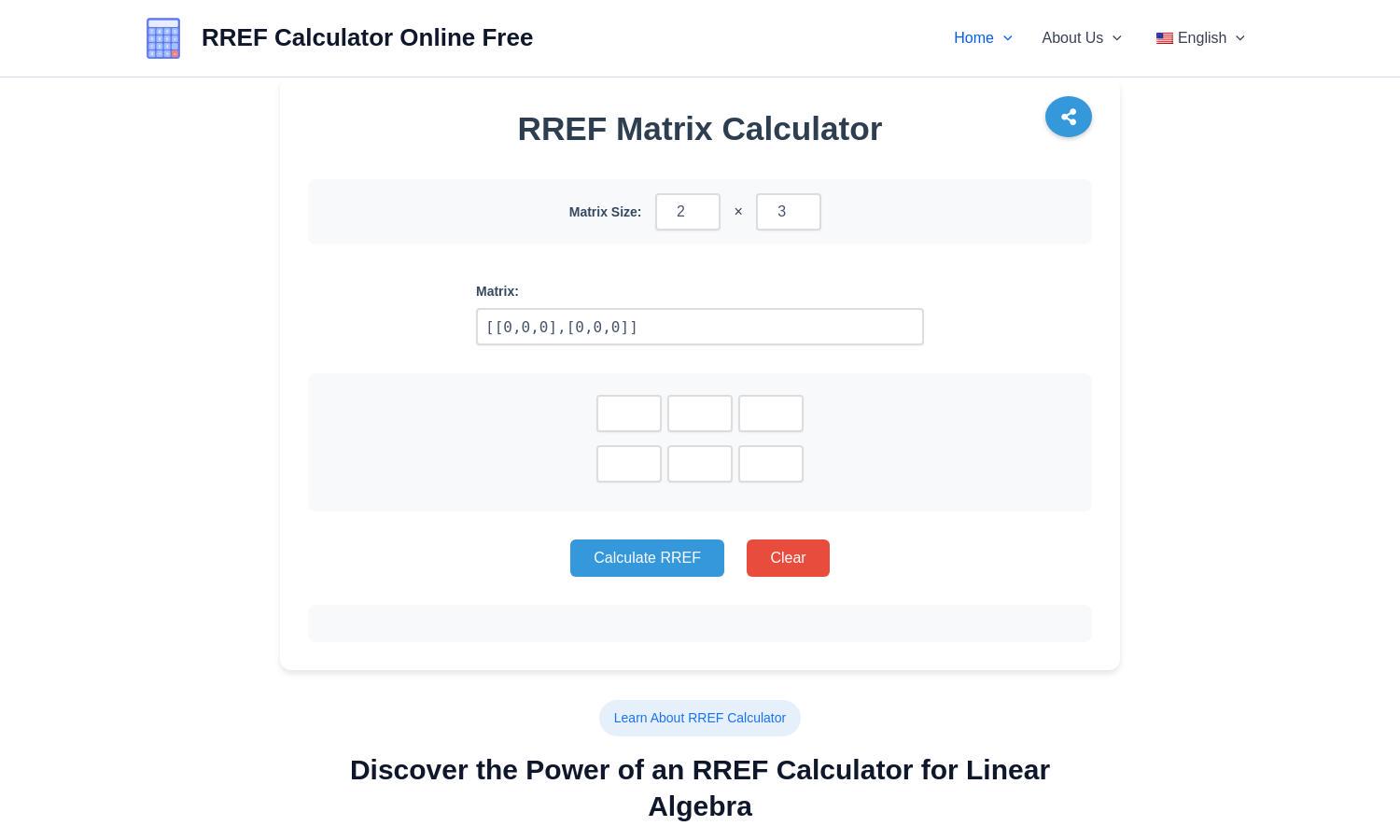
RREF Calculator
About RREF Calculator
RREF Calculator is an innovative online tool designed to convert matrices into Reduced Row Echelon Form effortlessly. Targeting students, educators, and professionals, it simplifies solving linear equations through clear step-by-step computations, enhancing accuracy and saving time in linear algebra tasks.
RREF Calculator offers a completely free service, ensuring users can compute RREF without any charges. There are no subscription tiers or additional costs, making it accessible to all, enhancing users' learning while enabling swift calculations and accurate results in linear algebra.
RREF Calculator features a user-friendly interface designed for seamless interaction. Its intuitive layout, quick input options, and instant result display make it accessible, allowing users to focus on learning rather than complicated matrix operations, ensuring an efficient experience in linear algebra.
How RREF Calculator works
Users engage with RREF Calculator by simply entering the dimensions and elements of their matrix into the provided fields. Upon clicking the “Calculate RREF” button, the tool employs the Gauss-Jordan elimination method to transform the matrix instantly into Reduced Row Echelon Form, streamlining linear equation solutions.
Key Features for RREF Calculator
Gauss-Jordan Elimination Method
The Gauss-Jordan elimination method is a key feature of RREF Calculator, allowing for quick matrix transformation into Reduced Row Echelon Form. This innovative process simplifies solving linear equations, making RREF Calculator an essential tool for students and professionals alike.
Step-by-Step Calculation Process
RREF Calculator's step-by-step calculation process enhances clarity by breaking down each transformation. Users can easily follow along with the changes made to their matrix, ensuring a deeper understanding of linear algebra concepts while benefiting from the tool’s precision.
Real-Time Calculation Results
RREF Calculator delivers real-time calculation results, providing users with immediate access to the Reduced Row Echelon Form of their matrices. This feature emphasizes efficiency and accuracy, allowing learners and professionals to quickly analyze and interpret their data without delay.